[출처 : 블로그 jxlovekjb님]
다양한 모습으로 나타나는 각 국의 건축물들의 특수성과
공통성은 다른 문화 예술품들보다
그 나라의 문화적 특성이 강하다.
때문에 동, 서양간의 미감의 차이가 있다면 그것에 대한
설명도 건축물이 가장 극명하게 보여주리라 생각한다.
백은비율은 우리 주위에 있으면서도 생소한 비율이다.
金剛(금강)이란 금강석,
즉 다이아몬드를 일컫는 우리말이다.
동양의 금강비는 황금보다 더 귀한 다이아몬드 같은
분할을 뜻한다.
서양에서는 황금분할이라는 황금비가 있다면
이보다 더 최고의 비율이 금강비이다.
금강비는 안정 뿐만 아니라 여유가 느껴지는
수학적 비례이다.
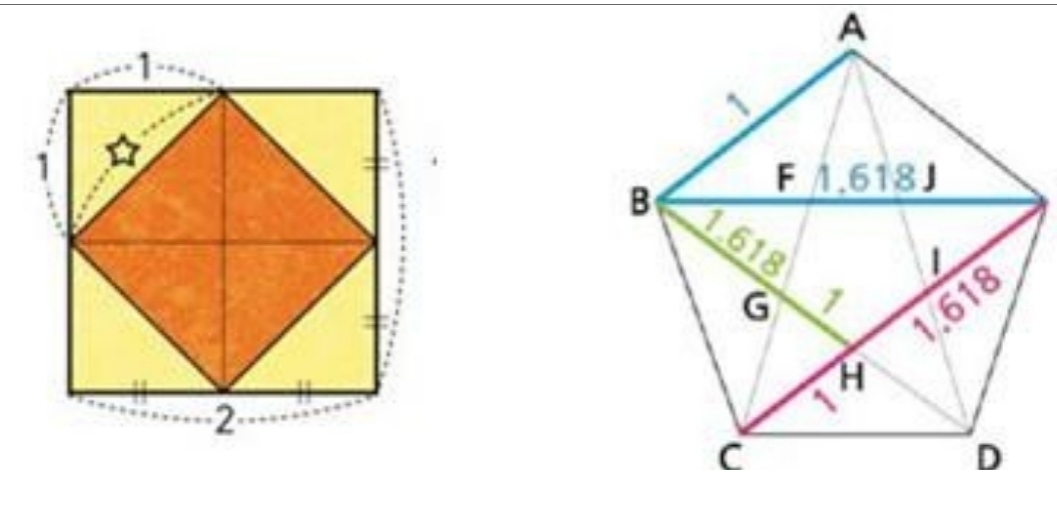
금강비와 황금비는 수학에서 말하는
루트와 파이(Φ, Phi)를 말한다.
금강비는 1: 루트2 = 1: 1.414...를 말하며,
황금비는 1:1.618...를 말한다.
따라서 금강비는 7등신이 되고, 황금비는 8등신이 된다.
금강비는 직각이등변삼각형의 구도이고 황금비는
정오각형의 한변의 길이와 대각선의 길이의 비를 말한다.
식물은 좀 더 안정적인 형태를 갖추면서
금강비례의 형태로 성장한다.
사람의 몸도 아름다움보다는 실용성을 추구하는 금강비례이다. 이는 안정감과 실용성,
편리함과 정적인 평화뿐만 아니라
미적 아름다움을 겸하고 있다.
A4용지 등에 사용되는 비율이 바로 백은비율이다
(금강비율이라고도 함).
금강비의 대표적인 건축물이 부석사 무량수전,
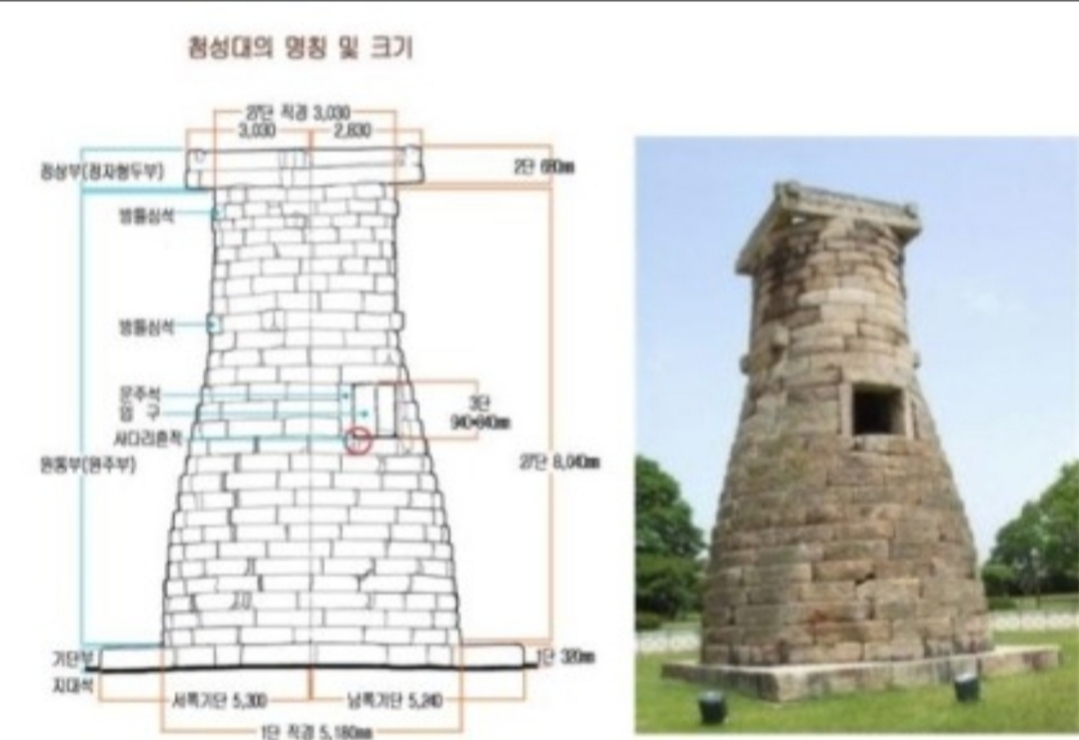
신라의 밤하늘을 바라보았던 첨성대,
즐거움과 흥의 문화의 발상지 포석정과 안압지이다.
첨성대는 밑단의 지름과 곡면의 기둥 상단까지의
높이의 비가 1: 1.414인 금강비이다.
포석정은 전체 크기에서
가로와 세로의 비율이 1:1.414이다.
안압지는 중심건물인 용왕전의 위치와
안압지 전체의 끝인 북쪽 호수 가장자리까지의
거리의 비가 1:1.414이다.
가장 오래된 목조 건축물 부석사 무량수전은
바닥면을 기준으로 용마루 높이까지의
가로와 세로의 비가 금강비이다.
그 내부 기둥의 높이와 두 기둥을 잇는
서까래의 길이의 비가 조화로운 금강비이다.
외부가 가로 61.9자(고려시대의 1자=32.21cm),
세로 38.2자로 직사각형인 무량수전은
황금비례(1.62 대 1)를 이룬다.
직사각형인 무량수전을 정사각형과
작은 직사각형으로 나누는 위치에 불단이 있다.
불단의 앞을 이은 선과 무량수전의 대각선이 만나는 점은
작은 직사각형을 더 작은 정사각형과 직사각형으로 나눈다.
이 과정을 반복하면 직사각형이 점점 작아지면서
시계방향으로 회전한다.
각 직사각형의 한 점을 이으면 ‘황금나선’이 나온다.
황금나선은 나팔꽃의 가지가 뻗어가는 모습이나
숫양의 뿔과 같이 자연 속에서 다양하게 발견할 수 있다.
경북궁 근정전은 바깥기둥을 기준으로 가로30.2m,
세로 21.2m로 금강비이다.
근정전은 두개의 단 위에 올려져 있는데,
아랫단 앞의 광장은 정사각형이다.
정사각형의 한 점에서 대각선 길이를 반지름으로
하는 원을 그리면 근정전 건물 앞부분에 닿는다.
이 대각선의 길이는 정사각형과 √2 비례관계를 보인다.
근정전의 위치가 근정전 일곽(一廓)과 금강비례를 이룬다
또한, A4의 대각선을 B4의 긴 변에 대어보면 꼭 맞는다.
그러면 A4와 B4의 면적 비는 1:1.5가 된다.
이는 백은비율에 의한 것이다.
A4의 가로(210mm), 세로(297mm)는 백은비율이다.
B4라고 그 예외는 아니다.
백은비는 보자기 등에도 활용된다.
이들은 정사각형인데,
한 변이 1인 정사각형의 대각선의 길이는
피타고라스의 정리에 의해 루트2가 되기 때문이다
A4와 B4등의 용지들에 숨어있는 소중하면서도 존재감 없는
비율이지만, 생활 속에는 깊숙히 파고들어 있는 것 같다.
훌륭한 비례는 편안함을 주고 나쁜 비례는 불편함을 준다
ㅡ